What is the Goal of RF PCB Impedance Matching?

RF circuits acting strangely? Signals weak or noisy? Mismatched impedances might be stealing your power and corrupting your data, a problem I've seen derail projects many times.

The primary goal of RF PCB impedance matching is to maximize power transfer between stages and minimize signal reflections. This ensures signal integrity by preserving the information content and energy efficiency of the RF signal.

It sounds straightforward, but as I've learned over nearly 20 years in hardware engineering, achieving good impedance matching means deeply understanding what goes wrong when it's ignored and how every tiny PCB feature can play a big role. Let's explore this critical aspect of RF design further, because it's not just about preventing power loss, but also about maintaining the signal-to-noise ratio¹ (\(SNR\)) and preventing issues like intersymbol interference (\(ISI\)) that can cripple a system.

---

What happens in an RF circuit if impedances are mismatched?

Designing an RF circuit but worried about performance? I've seen designs falter because mismatched impedances caused serious issues, degrading signal quality.

Mismatched impedances in RF circuits cause signal reflections, leading to power loss, reduced signal-to-noise ratio (\(SNR\)), and potential damage to components. Standing waves can also create damaging voltage peaks.

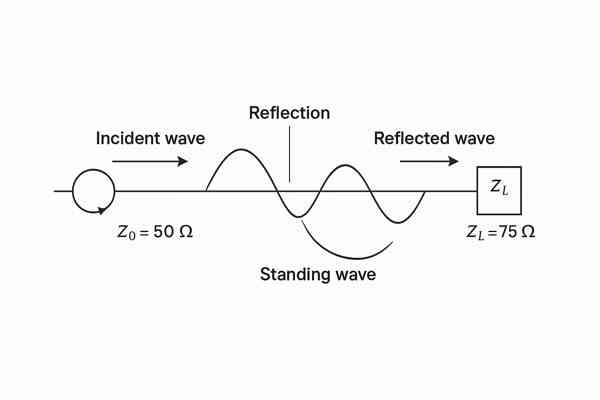
When an RF signal traveling along a transmission line encounters an interface with a different impedance, a portion of the signal's energy is reflected. This is a fundamental concept, but its implications are far-reaching in high-frequency design. The severity of this reflection is quantified by the reflection coefficient² (\(\Gamma\)) and the Voltage Standing Wave Ratio³ (\(VSWR\)). In an ideal world, we aim for \(\Gamma = 0\) and a \(VSWR\) of \(1:1\), meaning all power is transmitted. However, achieving perfection is rare. For instance, a \(VSWR\) of \(1.5:1\), which many might consider acceptable in some contexts, already means about 4% of your precious power is reflected. If it climbs to \(2.0:1\), that reflected power jumps to over 11.1%. I always refer to foundational texts like "Microwave Engineering" by David M. Pozar for the underlying equations.

This reflected power isn't just lost; it can cause several problems:

• Signal Distortion: The reflected waves can combine with the incident waves, creating constructive and destructive interference. This distorts the signal's amplitude and phase. In digital RF systems, this is a nightmare, leading to intersymbol interference⁴ (\(ISI\)), where one symbol blurs into the next, corrupting data. In analog systems, it can manifest as non-linearities and a general degradation of signal quality.
• Component Stress: The standing waves resulting from reflections create voltage and current maximums along the transmission line. These peaks can exceed the voltage ratings of sensitive components or cause excessive current leading to overheating, particularly in power amplifiers. I've debugged systems where mysterious PA failures were eventually traced back to severe mismatches.
• Frequency Instability: For components like oscillators, reflected power can "pull" the operating frequency, leading to instability and unpredictable behavior.
• Reduced Signal-to-Noise Ratio (\(SNR\)): Less power reaching the intended destination and the potential introduction of noise-like effects from reflections inherently degrade the \(SNR\). This is especially critical in receiver front-ends.

Here's a table to illustrate how \(VSWR\) impacts power transmission, derived from standard RF formulas you'd find in texts like "RF Circuit Design" by Chris Bowick:

\(VSWR\)	Reflection Coefficient (\(|\Gamma|\))	Return Loss (\(\text{dB}\))	Mismatch Loss (\(\text{dB}\))	% Reflected Power	% Transmitted Power
\(1.0:1\)	\(0.00\)	\(\infty\)	\(0.00\)	0.0	100.0
\(1.1:1\)	\(0.048\)	\(26.44\)	\(0.01\)	0.23	99.77
\(1.2:1\)	\(0.091\)	\(20.83\)	\(0.04\)	0.83	99.17
\(1.5:1\)	\(0.20\)	\(13.98\)	\(0.17\)	4.0	96.0
\(2.0:1\)	\(0.333\)	\(9.54\)	\(0.51\)	11.1	88.9
\(3.0:1\)	\(0.50\)	\(6.02\)	\(1.25\)	25.0	75.0

Understanding these consequences is the first step to appreciating why meticulous impedance matching is non-negotiable in RF PCB design.

---

How is microstrip trace width set for a 50-Ohm RF impedance?

Need a specific impedance for your RF traces? I've seen enough projects where "eyeballing" the trace width led to poor RF performance. Guessing won't cut it.

Microstrip trace width for a \(50-\Omega\) RF impedance depends critically on the PCB's dielectric constant (\(\epsilon_r\)), the height of the dielectric (\(h\)) above the ground plane, and the trace copper thickness (\(t\)). Specialized calculators or validated formulas are essential.

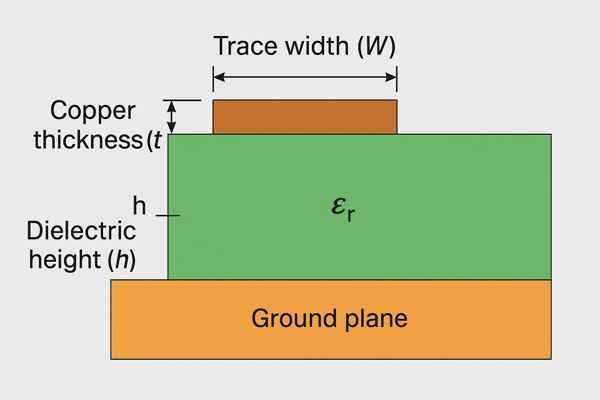
Calculating the correct trace width for a target impedance, typically \(50 \Omega\) in many RF systems, is a core task in PCB design. The characteristic impedance⁵ (\(Z_0\)) of a microstrip line⁶ – a trace routed on an outer layer with a ground plane beneath it – is governed by several physical parameters. While complex field solvers provide the most accurate results, well-established approximation formulas exist, such as those from IPC-2141. For practical work, EDA tools or dedicated calculators are indispensable. Standard FR-4 typically has an \(\epsilon_r\) ranging from about \(4.2\) to \(4.8\) at RF frequencies. RF-specific laminates like Rogers RO4350B (with \(\epsilon_r \approx 3.48 \pm 0.05\) as per Rogers Corporation datasheets) offer tighter control. Copper thickness (\(t\)) is usually specified in ounces (e.g., \(0.5 \text{ oz} = 17.5 \text{ µm}\), \(1 \text{ oz} = 35 \text{ µm}\)). A widely cited approximation for microstrip impedance is \(Z_0 \approx \frac{87}{\sqrt{\epsilon_r + 1.41}} \ln\left(\frac{5.98h}{0.8W + t}\right) \Omega\).

Let's look at how trace width (\(W\)) for a \(50 \Omega\) microstrip might change with different dielectric heights (\(h\)) or materials (\(\epsilon_r\)), assuming \(1 \text{ oz}\) copper (\(t = 0.035 \text{ mm}\)). These values are illustrative and calculated using a standard microstrip impedance formula.

Parameter Changed	Material \(\epsilon_r\)	Dielectric Height (\(h\))	Approx. Trace Width (\(W\)) for \(50 \Omega\)	Notes
Baseline	\(4.4\) (FR-4)	\(0.2 \text{ mm}\) (\(7.87 \text{ mils}\))	\(\approx 0.36 \text{ mm}\) (\(14.2 \text{ mils}\))	Common multilayer stackup
Increased Height	\(4.4\) (FR-4)	\(0.5 \text{ mm}\) (\(19.7 \text{ mils}\))	\(\approx 0.92 \text{ mm}\) (\(36.2 \text{ mils}\))	Width increases significantly with height
Decreased Height	\(4.4\) (FR-4)	\(0.1 \text{ mm}\) (\(3.9 \text{ mils}\))	\(\approx 0.17 \text{ mm}\) (\(6.7 \text{ mils}\))	Width decreases for thinner dielectrics
RF Substrate	\(3.48\) (Rogers RO4350B)	\(0.2 \text{ mm}\) (\(7.87 \text{ mils}\))	\(\approx 0.44 \text{ mm}\) (\(17.3 \text{ mils}\))	Lower \(\epsilon_r\) requires wider trace
Thicker 2-layer Board	\(4.4\) (FR-4)	\(1.524 \text{ mm}\) (\(60 \text{ mils}\))	\(\approx 2.85 \text{ mm}\) (\(112 \text{ mils}\))	Common for basic prototypes, very wide trace

(Source for \(\epsilon_r\) of RO4350B: Rogers Corporation datasheet. Other calculations based on Wheeler/IPC formulas.)

As you can see, trace width (\(W\)) is highly sensitive to both the dielectric constant⁷ (\(\epsilon_r\)) and its height (\(h\)). This is why obtaining accurate stackup information from your PCB fabricator is absolutely critical. During the Tuxedo Keypad project at Honeywell, we had to manage designs across different manufacturing sites, and ensuring consistent stackups for our Wi-Fi module's RF traces was a constant point of attention to maintain performance.

---

What PCB feature primarily defines stripline impedance?

Working with internal RF traces where signals are sandwiched between ground planes? Understanding stripline impedance is absolutely crucial for maintaining signal integrity deep within your PCB.

Stripline impedance is primarily defined by the trace width (\(W\)), the total dielectric thickness (\(b\)) between the two ground planes, and the dielectric constant (\(\epsilon_r\)) of the material uniformly surrounding the trace.

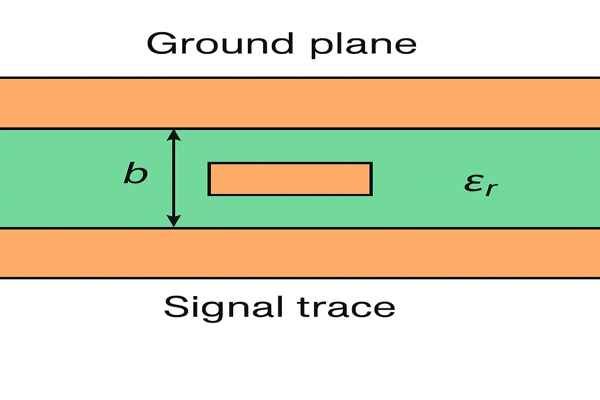
A stripline configuration places the signal trace on an internal layer, with solid ground planes directly above and below it, all embedded within a uniform dielectric material. This structure offers excellent signal isolation. Key parameters determining its characteristic impedance (\(Z_0\)) include the dielectric constant (\(\epsilon_r\)), separation between ground planes (\(b\)), trace width (\(W\)), and trace thickness (\(t\)). For practical calculations, formulas from IPC-2141A⁸ or EDA tools are recommended.

Here's an illustrative table showing how stripline trace width (\(W\)) for a \(50 \Omega\) line might vary, assuming \(1 \text{ oz}\) copper (\(t = 0.035\text{mm}\)) and a centered trace.

Parameter Changed	Material \(\epsilon_r\)	Dielectric Thickness (\(b\)) between planes	Approx. Trace Width (\(W\)) for \(50 \Omega\)	Notes
Baseline	\(3.38\) (Rogers RO4003C)	\(0.508 \text{ mm}\) (\(20 \text{ mils}\))	\(\approx 0.38 \text{ mm}\) (\(15.0 \text{ mils}\))	Typical RF material and stackup
Thicker Dielectric	\(3.38\) (Rogers RO4003C)	\(0.813 \text{ mm}\) (\(32 \text{ mils}\))	\(\approx 0.63 \text{ mm}\) (\(24.8 \text{ mils}\))	Width increases with plane separation
FR-4 Material	\(4.2\) (FR-4 like)	\(0.508 \text{ mm}\) (\(20 \text{ mils}\))	\(\approx 0.33 \text{ mm}\) (\(13.0 \text{ mils}\))	Higher \(\epsilon_r\) requires narrower trace
Very Thin Dielectric	\(3.38\) (Rogers RO4003C)	\(0.203 \text{ mm}\) (\(8 \text{ mils}\))	\(\approx 0.14 \text{ mm}\) (\(5.5 \text{ mils}\))	Narrow trace for thin core

(Source for \(\epsilon_r\) of RO4003C: Rogers Corporation datasheet. Calculations based on IPC-2141A formulas for centered stripline.)

It's crucial to ensure the trace is accurately centered between the ground planes; an offset trace becomes an "offset stripline" with different impedance characteristics. The controlled dielectric environment in stripline generally offers better impedance stability over frequency compared to microstrip.

---

Which passive components form a basic RF matching network?

Need to bridge the gap between different impedances in your RF design? Often, it's the humble passive components that are the key to a successful match.

Basic RF matching networks primarily use passive components like inductors (\(L\)) and capacitors (\(C\)). Resistors (\(R\)) are sometimes strategically included, typically for broadband matching or to provide necessary attenuation.

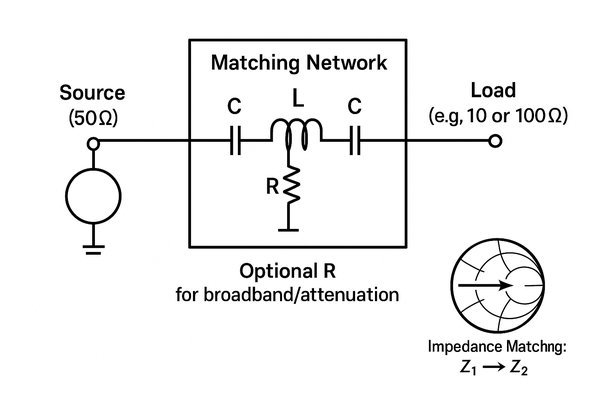
When I'm faced with an impedance mismatch, my first thought often goes to creating a matching network using inductors (\(L\)) and capacitors (\(C\)). These components are reactive, meaning they store energy and can introduce phase shifts to transform impedances. Here's a summary of their roles:

Component	Symbol	Impedance (\(Z\))	Primary Role in Matching	Typical RF Values Example
Inductor	\(L\)	\(j\omega L = j2\pi fL\)	Adds positive reactance; impedance increases with frequency.	\(0.5 \text{ nH} - 100 \text{ nH}\) (e.g., \(3.3 \text{ nH}\) @ \(2\text{GHz}\))
Capacitor	\(C\)	\(\frac{1}{j\omega C}\)	Adds negative reactance; impedance decreases with frequency.	\(0.1 \text{ pF} - 100 \text{ pF}\) (e.g., \(1.0 \text{ pF}\) @ \(2\text{GHz}\))
Resistor	\(R\)	\(R\)	Adds real impedance; dissipates power; used for broadbanding or attenuation.	\(10 \Omega - 1 \text{ k}\Omega\)

Common L-C network topologies include \(L\)-networks, \(\Pi\)-networks, and \(T\)-networks. When selecting these components for RF, parasitics like Self-Resonant Frequency⁹ (\(SRF\)) for inductors and Equivalent Series Resistance (\(ESR\)) for capacitors are critical. For example, an inductor's \(SRF\) must be well above the operating frequency. A typical \(10\text{nH}\) chip inductor might have an \(SRF\) of \(6 \text{ GHz}\), making it suitable for applications below that, while a \(100\text{nH}\) inductor might have an \(SRF\) closer to \(1.5 \text{ GHz}\) (values from Murata or Coilcraft datasheets). High-\(Q\) components are preferred for narrow-band, low-loss matching.

---

How are L-C matching network component values chosen?

Knowing you need an \(L\)-\(C\) network to bridge an impedance gap is the first step. But the critical question follows: how do you actually determine the right inductance (\(L\)) and capacitance (\(C\)) values?

\(L\)-\(C\) matching network component values are chosen using tools like the Smith Chart, analytical formulas derived from network theory (often involving a target \(Q\)-factor), or with the aid of RF simulation software.

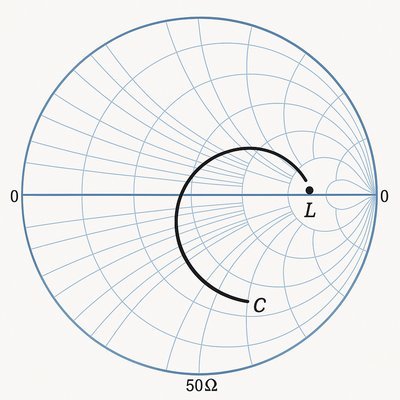
The core objective is to transform a given load impedance (\(Z_L = R_L + jX_L\)) to a desired input impedance (\(Z_S = R_S + jX_S\)), often \(50 \Omega\). The \(L\)-network is the simplest, using two reactive components.
On a Smith Chart¹⁰, you normalize the load impedance (e.g., \(z_L = \frac{Z_L}{50\Omega}\)) and plot it. Then, reactive elements are added to move towards the matched point (typically \(1+j0\)). From the normalized reactances, component values are calculated using \(L = \frac{X_L}{2\pi f}\) or \(C = \frac{1}{2\pi f X_C}\).
Analytically, for an \(L\)-network matching real resistances, the Quality Factor¹¹ (\(Q\)) is often a starting point: \(Q = \sqrt{\frac{R_{big}}{R_{small}} - 1}\). The series (\(X_{ser}\)) and shunt (\(X_{sh}\)) reactance magnitudes are \(|X_{ser}| = Q \cdot R_{small}\) and \(|X_{sh}| = \frac{R_{big}}{Q}\).
For instance, to match a \(10 \Omega\) source to a \(50 \Omega\) load at \(1 \text{ GHz}\) with a low-pass \(L\)-network: \(Q = \sqrt{\frac{50}{10} - 1} = 2\). Then \(|X_{serL}| = 2 \cdot 10 = 20 \Omega \Rightarrow L = \frac{20}{2\pi \cdot 1 \cdot 10^9} \approx 3.18 \text{ nH}\). And \(|X_{shC}| = \frac{50}{2} = 25 \Omega \Rightarrow C = \frac{1}{25 \cdot 2\pi \cdot 1 \cdot 10^9} \approx 6.37 \text{ pF}\).

Here's a table summarizing common L-Network applications for transforming \(R_1\) to \(R_2\):

Transformation	Series Element	Shunt Element	Filter Type	Notes (\(Q = \sqrt{\frac{R_{high}}{R_{low}} - 1}\))
\(R_{low} \to R_{high}\)	\(L\) (series \(X_S = Q R_{low}\))	\(C\) (shunt \(X_P = \frac{R_{high}}{Q}\))	Low-Pass	Places \(L\) in series with \(R_{low}\), \(C\) in shunt with \(R_{high}\)
(\(R_{low}\) at input)	\(C\) (series \(X_S = Q R_{low}\))	\(L\) (shunt \(X_P = \frac{R_{high}}{Q}\))	High-Pass	Places \(C\) in series with \(R_{low}\), \(L\) in shunt with \(R_{high}\)
\(R_{high} \to R_{low}\)	\(C\) (shunt \(X_P = \frac{R_{high}}{Q}\))	\(L\) (series \(X_S = Q R_{low}\))	Low-Pass	Places \(C\) in shunt with \(R_{high}\), \(L\) in series with \(R_{low}\)
(\(R_{high}\) at input)	\(L\) (shunt \(X_P = \frac{R_{high}}{Q}\))	\(C\) (series \(X_S = Q R_{low}\))	High-Pass	Places \(L\) in shunt with \(R_{high}\), \(C\) in series with \(R_{low}\)

(Reactances \(X_S\), \(X_P\) are magnitudes; \(L = \frac{X}{2\pi f}\), \(C = \frac{1}{X \cdot 2\pi f}\)). These formulas are standard and found in texts like "RF Circuit Design" by Chris Bowick or the ARRL Handbook. RF simulation software (ADS, AWR, QucsStudio) is extremely helpful for optimizing these values and including parasitics, aiming for goals like \(S11 < -20 \text{ dB}\). My experience debugging the PACE evaluation board at Lightelligence under extreme time pressure highlighted how crucial accurate simulation, including parasitics, can be before committing to hardware.

---

When is a quarter-wave transmission line used for RF matching?

Can a simple PCB trace, just by its length and width, act as a matching element? Absolutely. The quarter-wave transformer is a classic and elegant RF technique I've used for specific scenarios.

A quarter-wave transmission line is used for RF matching primarily when transforming one real (purely resistive) impedance to another real impedance. It's most effective over a relatively narrow frequency band centered at its quarter-wavelength (\(\frac{\lambda_g}{4}\)) frequency (\(f_0\)).

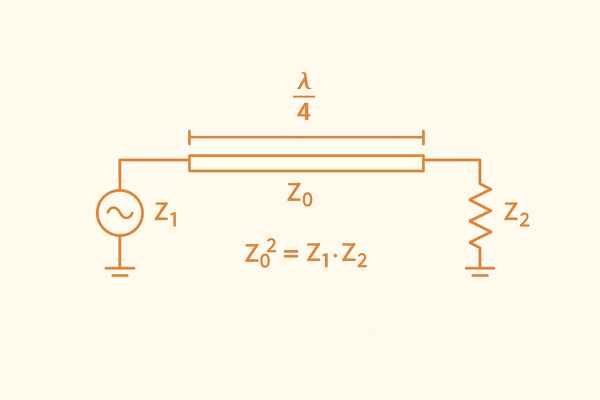
The magic of a quarter-wave transmission line lies in its impedance-inverting property. A segment of transmission line with characteristic impedance \(Z_Q\), terminated with a load \(Z_L\), has an input impedance \(Z_{in} = \frac{Z_Q^2}{Z_L}\). To match a source \(R_S\) to a load \(R_L\), the required \(Z_Q = \sqrt{R_S \cdot R_L}\). The physical length \(L_{phys} = \frac{\lambda_g}{4} = \frac{(\frac{\lambda_0}{\sqrt{\epsilon_{eff}}})}{4}\), where \(\lambda_0 = \frac{c}{f_0}\) is the free-space wavelength and \(\epsilon_{eff}\) is the effective dielectric constant. For instance, at \(f_0 = 2 \text{ GHz}\), \(\lambda_0 = \frac{3 \times 10^8 \text{ m/s}}{2 \times 10^9 \text{ Hz}} = 150 \text{ mm}\). If \(\epsilon_{eff} \approx 3.2\), then \(\lambda_g \approx \frac{150 \text{ mm}}{\sqrt{3.2}} \approx 83.85 \text{ mm}\). So, \(L_{phys} \approx \frac{83.85 \text{ mm}}{4} \approx 20.96 \text{ mm}\).

Here's a summary of its characteristics:

Feature	Description
Principle	Transforms \(Z_{in} = \frac{Z_Q^2}{Z_L}\). For \(R_S\) to \(R_L\), \(Z_Q = \sqrt{R_S \cdot R_L}\).
Advantages	- Low loss (if implemented with low-loss line). - Simple to implement on PCB (no discrete components). - Can be integrated into filter structures.
Disadvantages	- Matches real-to-real impedances primarily. - Narrowband performance (typically 10-20% for \(VSWR < 1.5:1\), per Pozar's "Microwave Engineering"). - Can be physically long at lower RF frequencies (e.g., < 500 MHz). - Fixed transformation ratio once designed.
Example	To match \(50\Omega\) to \(100\Omega\): \(Z_Q = \sqrt{50 \cdot 100} \approx 70.7\Omega\). Line length is \(\frac{\lambda_g}{4}\) at \(f_0\).

Despite limitations, for specific antenna feeds or inter-stage matching where conditions are right, it's a very effective technique.

---

How can a shorted RF stub create a specific reactance?

Need to introduce a precise amount of inductance or capacitance into your RF circuit without using a discrete component? A shorted transmission line stub can be an elegant and practical solution on a PCB.

A shorted RF stub, which is simply a transmission line section short-circuited at its far end, presents a purely reactive impedance (either inductive or capacitive) at its input. This reactance is determined by the stub's characteristic impedance (\(Z_0\)) and its electrical length (\(\theta = \beta l\), where \(\beta = \frac{2\pi}{\lambda_g}\)) relative to the signal wavelength.

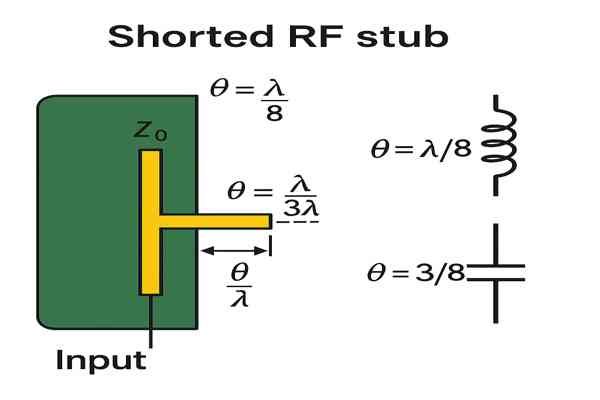
The input impedance of a lossless shorted stub (\(Z_L=0\)) is \(Z_{in} = jZ_0 \tan(\beta l)\). This shows \(Z_{in} = jX_{in}\) where \(X_{in} = Z_0 \tan(\beta l)\). Its behavior is summarized below:

Stub Length (\(l\))	Phase Length (\(\beta l\))	\(\tan(\beta l)\)	Input Impedance (\(Z_{in}\))	Behaves As	Example Value (for \(Z_0=50\Omega\))
\(l = 0\)	\(0\)	\(0\)	\(0\)	Short Circuit	\(0 \Omega\)
\(0 < l < \frac{\lambda_g}{4}\)	\(0 \to \frac{\pi}{2}\)	\(0 \to +\infty\)	\(+j0 \to +j\infty\)	Inductor	\(l=\frac{\lambda_g}{8} \Rightarrow +j50\Omega\)
\(l = \frac{\lambda_g}{4}\)	\(\frac{\pi}{2}\)	\(+\infty\)	\(+j\infty\)	Parallel Resonant Circuit (Open to series)	Infinite
\(\frac{\lambda_g}{4} < l < \frac{\lambda_g}{2}\)	\(\frac{\pi}{2} \to \pi\)	\(-\infty \to 0\)	\(-j\infty \to -j0\)	Capacitor	\(l=\frac{3\lambda_g}{8} \Rightarrow -j50\Omega\)
\(l = \frac{\lambda_g}{2}\)	\(\pi\)	\(0\)	\(0\)	Series Resonant Circuit (Short to series)	\(0 \Omega\)

(Theoretical basis from texts like "Fields and Waves in Communication Electronics" by Ramo, Whinnery, and Van Duzer.) For instance, to create an inductive reactance of \(+j70 \Omega\) at \(2.45 \text{ GHz}\) using a \(Z_0 = 70 \Omega\) stub, we need \(\tan(\beta l) = 1\), so \(\beta l = \frac{\pi}{4}\), meaning \(l = \frac{\lambda_g}{8}\). If \(\epsilon_{eff} \approx 3.0\), \(\lambda_g \approx \frac{122.4 \text{ mm}}{\sqrt{3.0}} \approx 70.7 \text{ mm}\), so \(l \approx \frac{70.7 \text{ mm}}{8} \approx 8.84 \text{ mm}\).

---

What is a practical challenge in RF matching network PCB layout?

Designing the theoretically perfect matching network on paper or in simulation is one thing. But as I've experienced many times, translating that into a physical PCB layout introduces a host of real-world challenges that can detune your carefully calculated network.

A significant practical challenge in RF matching network PCB layout is meticulously managing and minimizing parasitic reactances introduced by component pads, vias, trace segments, and even component spacing. These un-designed parasitics can significantly alter the network's performance from its intended response.

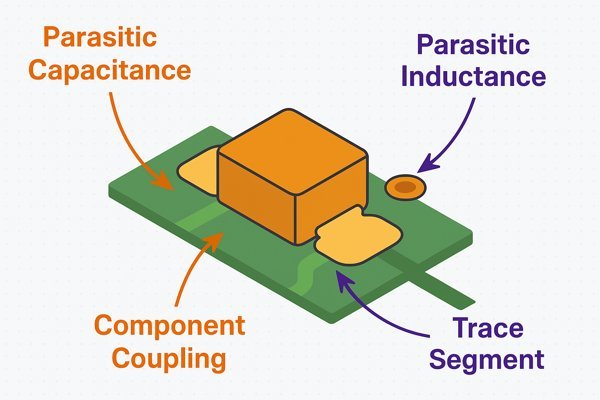
When working with RF frequencies, every millimeter matters. For example, an \(0402\) component pad can add \(0.05 \text{ pF}\) to \(0.2 \text{ pF}\) of capacitance. If your design uses a \(1 \text{ pF}\) capacitor, this is a significant error. A typical via (\(0.2\text{mm}\) drill, \(1.6\text{mm}\) board) might have \(0.4 \text{ nH}\) to \(0.8 \text{ nH}\) of inductance. Short traces add inductance (\(\approx 0.6 - 1.0 \text{ nH/mm}\)) and capacitance (\(\approx 0.05 - 0.1 \text{ pF/mm}\)). If a design needs a \(0.5 \text{ nH}\) inductor, and parasitics add \(0.2 \text{ nH}\), the discrete part should be \(0.3 \text{ nH}\).

Here's a table summarizing common parasitic elements:

Parasitic Source	Typical Reactance Type	Estimated Value Range (Illustrative for RF)	Potential Impact	Mitigation Strategy
SMD Component Pad (e.g., \(0402\))	Shunt Capacitance	\(0.05 - 0.2 \text{ pF}\) (to ground)	Detunes network, shifts resonant frequencies	Smaller pads, thicker dielectric, EM simulation
	Series Inductance	\(0.1 - 0.3 \text{ nH}\) (along pad length)	Adds series \(L\), shifts phase	Shorter pads, wider pads (can increase \(C\))
Via (e.g., \(0.2\text{mm}\) drill, \(1.6\text{mm}\) board)	Series Inductance	\(\approx 0.4 - 0.8 \text{ nH}\)	Limits grounding effectiveness for shunt parts	Multiple vias ("via stitching"), shorter/wider vias, minimize use
	Shunt Capacitance	\(\approx 0.1 - 0.3 \text{ pF}\) (to planes, via anti-pad)	Can be significant in dense designs	Proper anti-pad sizing
Short Interconnecting Trace	Series Inductance	\(\approx 0.6 - 1.0 \text{ nH/mm}\)	Adds unwanted series \(L\)	Minimize trace lengths, use coplanar structures carefully
	Shunt Capacitance	\(\approx 0.05 - 0.1 \text{ pF/mm}\) (to ground)	Adds unwanted shunt \(C\)	Route over thicker dielectric if possible, minimize length
Component-to-Component Spacing	Mutual Coupling (\(L, C\))	Variable, depends on proximity, orientation, frequency	Unintended signal paths, detuning	Maintain adequate spacing, orthogonal placement if needed

(Values are estimates; actuals depend heavily on specific geometry, materials, and frequency. Refer to E. Bogatin's "Signal and Power Integrity - Simplified" for detailed discussions.)
If these parasitics are not anticipated, the matching network will likely require extensive bench tuning. For critical designs, especially above \(1-2 \text{ GHz}\), I always advocate for 3D electromagnetic (EM) simulation¹² of the layout (Ansys HFSS, CST Studio Suite) to capture these effects accurately.

---

How is RF matching network effectiveness practically tested?

Your RF matching network has been meticulously designed with calculations or simulation, and the PCB has been fabricated and assembled. But how do you actually confirm, with real hardware, that it's performing as intended?

RF matching network effectiveness is practically tested using a Vector Network Analyzer (VNA). The VNA measures key S-parameters, primarily the input return loss (\(S11\)) and sometimes the transmission gain/loss (\(S21\)), across the network's operational frequency band.

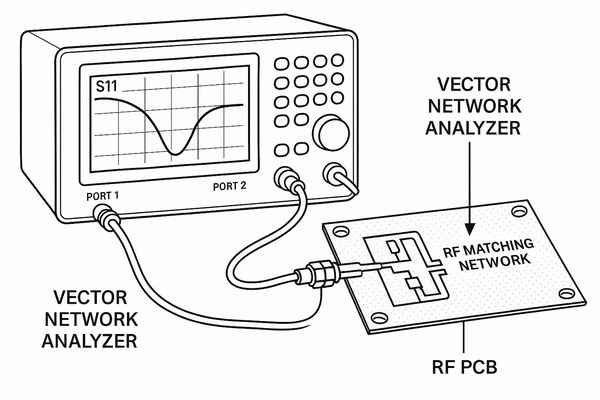
The Vector Network Analyzer (VNA)¹³ is the cornerstone of RF characterization. After careful calibration (SOLT - Short, Open, Load, Thru), the VNA measures S-parameters¹⁴. For example, an \(S11\) of \(-10 \text{ dB}\) means 10% power is reflected (\(VSWR \approx 1.92:1\)). Often, a target is \(S11 < -15 \text{ dB}\) (\(3.2\text{\%}\) power reflected, \(VSWR \approx 1.43:1\)) or even \(S11 < -20 \text{ dB}\) (\(1\text{\%}\) power reflected, \(VSWR \approx 1.22:1\)). The insertion loss¹⁵ (\(S21\)) should be minimized (e.g., \(< 0.5 \text{ dB}\)).

S-Parameter	Name	Description	Ideal Value for Good Match (Passive Network)	Common Target (\(\text{dB}\) or ratio)
\(S11\)	Input Return Loss	Ratio of reflected power to incident power at Port 1. Lower is better.	\(-\infty \text{ dB}\)	\(< -10 \text{ dB}\), pref. \(< -15 \text{ dB}\)
\(S21\)	Forward Gain/Loss	Ratio of power at Port 2 to power at Port 1. For passive match, this is loss.	\(0 \text{ dB}\)	\(< 0.5 \text{ dB}\) (loss)
\(S22\)	Output Return Loss	Ratio of reflected power to incident power at Port 2 (if applicable).	\(-\infty \text{ dB}\)	\(< -10 \text{ dB}\)
\(VSWR\)	Voltage Standing Wave Ratio	Derived from \(S11\) (\(VSWR = \frac{1 + |S11|}{1 - |S11|}\)). Lower is better.	\(1:1\)	\(< 2:1\), pref. \(< 1.5:1\)

My work on the Tuxedo Keypad's Wi-Fi module involved countless hours on the VNA, tweaking matching networks for antennas and filters to meet stringent FCC and CE certification requirements. Leading VNA manufacturers include Keysight, Rohde & Schwarz, and Anritsu.

---

Does solder mask thickness influence controlled RF impedance?

In the meticulous world of RF PCB design, I've learned that even seemingly minor details can have an impact. So, a common question arises: could something as ubiquitous as the solder mask layer actually affect your carefully designed controlled impedance traces?

Yes, solder mask thickness and its dielectric constant (\(\epsilon_r\)) do influence controlled RF impedance, particularly for microstrip lines. The solder mask alters the effective dielectric constant (\(\epsilon_{eff}\)) in the region immediately surrounding the trace, thereby changing its impedance.

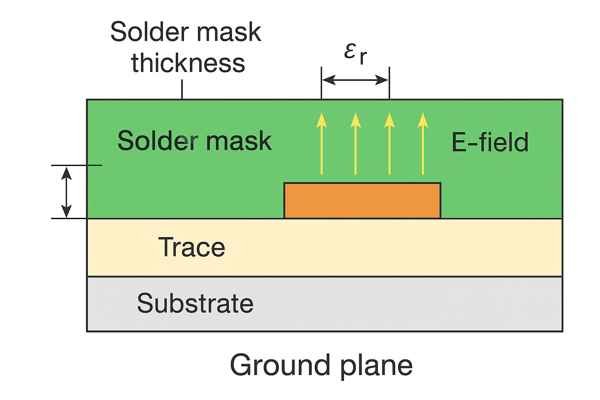
Solder mask (LPI typical \(\epsilon_r \approx 3.0 - 4.0\), thickness \(\approx 0.5 - 1.5 \text{ mils}\) over traces, per IPC-SM-840D) replaces air (\(\epsilon_r \approx 1\)) above a microstrip trace. This increases the overall \(\epsilon_{eff}\), which in turn decreases the characteristic impedance (\(Z_0 \propto \frac{1}{\sqrt{\epsilon_{eff}}}\)).

Here's how different aspects of solder mask can influence a microstrip line designed for \(50\Omega\) (bare copper):

Solder Mask Parameter Change	Typical Range/Value	Effect on Microstrip \(Z_0\)	Reason	Estimated \(Z_0\) Change (from bare \(50\Omega\))
Addition of Standard Solder Mask	\(1 \text{ mil}\) (\(25.4\text{µm}\)) thick, \(\epsilon_r \approx 3.5\)	Decrease	Increases overall \(\epsilon_{eff}\) as air (\(\epsilon_r=1\)) is replaced by mask (\(\epsilon_r > 1\))	\(1 - 3 \Omega\) lower (e.g., to \(47-49\Omega\))
Increase in Solder Mask Thickness (over trace)	From \(0.5 \text{ mil}\) to \(1.5 \text{ mil}\)	Further Decrease	More dielectric material with \(\epsilon_r > 1\) influences the fringing fields	Additional \(\approx 0.5 - 1 \Omega\) decrease
Increase in Solder Mask \(\epsilon_r\)	From \(\epsilon_r=3.0\) to \(\epsilon_r=4.0\)	Further Decrease	Higher \(\epsilon_r\) of mask material contributes more to increasing \(\epsilon_{eff}\) more	Additional \(\approx 0.5 - 1 \Omega\) decrease
Removal of Solder Mask (Solder Mask Opening)	N/A (bare copper)	Increase (back to design)	Reduces \(\epsilon_{eff}\) by exposing trace to air	Recovers original design impedance

(Estimates are illustrative and vary with specific trace geometry and substrate. Accurate modeling requires EM simulators or specialized calculators from sources like Polar Instruments).
For critical RF designs (e.g., \(> 5 \text{ GHz}\) or tight \(Z_0\) tolerance), solder mask effects must be included in simulations. For striplines, the effect is generally negligible as the field is contained internally.

---

Conclusion

In my experience, effective RF impedance matching is absolutely fundamental. It's the key to ensuring maximum power transfer, preserving vital signal integrity, and preventing data corruption in today's demanding high-frequency circuits.

---